Fractal Craft
Note: This is an entry for the GMTK Game Jam 2025. We've already begun working on a full release for this game. Stay tuned!
What do you see when you point a camera at its own video feed? The answer is infinity.
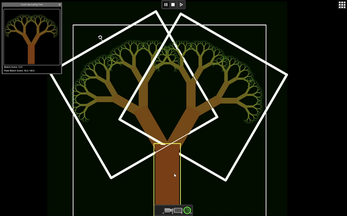
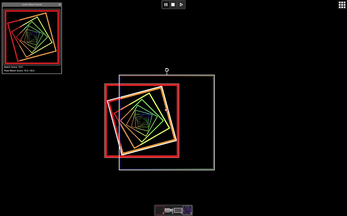
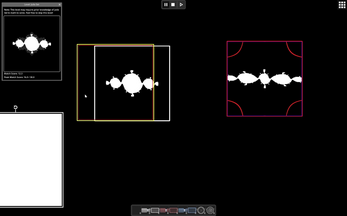
Fractal Craft is a puzzle game about constructing various fractal shapes using a technique called "video feedback loop" (a camera capturing transformed versions of its own output image). You complete levels by constructing the requested image using basic shapes, cameras, displays, and lenses.
IMPORTANT: If you don't want to be spoiled of the puzzle solutions, try the game first before watching the gameplay video!
Unfortunately, we didn't have enough time to make enough levels to explore all the mechanics, and the difficulty curve may not be reasonable. Feel free to skip a level if you get stuck.
Known Issues:
- The last level requires knowledge about Julia Sets in math to solve. This video by Matt Parker could be helpful.
- In the last level, the magenta edges meant only for visual indication also show up in the warped image of the lens. This is only a visual bug; it doesn't affect the rendering of the image captured by the cameras.
Credits:
Comments
Log in with itch.io to leave a comment.
Very Interesting and creative game
How do you zoom out?
Just mouse wheel. Is it not working for you?
I figured it out don't worry
A very unique and cool puzzle. The use of overlapping cameras and display are fascinating. I love a few puzzles, like the trees one. It really blows my mind of one how it works.
However, I also want to point out a few challenges on making a puzzle game like this.
1/ Understanding.
A puzzle game is built on the understanding on how two things work, and then let the player combine them togethere to find the solution, the so-called 'aha' moment.
Therefore it is important to understand the concept or underlying working of something. The harder a concept is to grasp, the better a tutorial should be for the player to understand it. And for a game like this, the tutorial should be extremely polished and thoughout.
(Imagine Baba is You, or Viewfinder without the first few levels.)
The concept of viewpoint and overlapping display are inherited simple but hard to grasp, because there are too much moving part in a single puzzle. For example, in a multiple display setting, how a part behaves after moving a display is hard to graps because when you move something, a lot of other things shift.
I would love to see how you guys tackles this design problem.
P/S: Including a math problem in a puzzle is generally fine, but your tutorial really need to improve so that player
Overall, a solid puzzle game. 8.5/10
Idea: 9/10
-Fun: 8/10
-Potential: 10/10
(Unique: 10/10)
Excution: 7.5
-Game Feel / Polish: 9/10
-Game Flow / Difficulty: 6/10
Thanks for the detailed feedback!
Agreed! There are quite a few quirks that can be confusing (e.g., unlike real displays, the display in this game actually has a transparency channel). Also, we've planned more complex mechanics for the later levels, so some well-designed tutorial levels are definitely going to be a critical part of the problem-solving experience.
cool game
I loved it but I do wish there were more levels <3
Thanks for playing!
This is just a jam entry. We've already started working on a full release. Probably with hundreds of levels! Stay tuned!
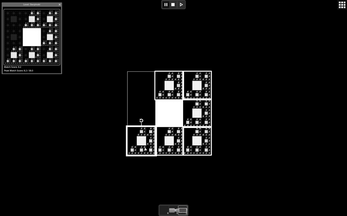
clever and super interesting! Although the 'sierpenski' levels aren't really sierpenski...that's the Menger Sponge.
Which I now just learned is also called the sierpenski cube! Neat! :)
Yeah, apparently only the 3D versions are called Merger Sponge. The 2D versions are called the Sierpiński Carpet. (While coding it, I actually named the files "Merger Carpet" at first, but changed it later when I learned that's not a thing haha)
sierpenski needs his carpet patched up -- It's full of holes.
Actually, bigger problem: there is no carpet -- its area is zero :)
hmm. It would appear so; if you think of it as "take any point, is there a hole there". However... If you think about it, each iteration, you remove 1/9 of the area, and 1/9 is less every time, which seems like it would approach a finite value. But another way to think of it is that the total carpet area at iteration n is 8/9 (n-1). This is always less and less continually. And sure enough, a sequence calculator says it approaches 0.
confusing...
Wikipedia has the last word:
The area of the carpet is zero (in standard Lebesgue measure).
Proof: Denote as ai the area of iteration i. Then ai + 1 = 8/9ai. So ai = (8/9)i, which tends to 0 as i goes to infinity.
I guess the only way to really tell is to make one, or steal Sierpenski's and weigh it. :)
Such a clever game! Well done
Super fun!